Disclaimer: These are personal notes and are not meant to be authoritative

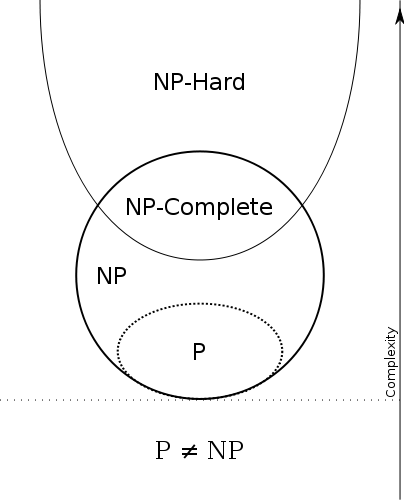
Computatioinal hardness is a measure of how efficiently an algorithm can run to solve a problem. Efficiency in this context is computational complexity. Understanding hardness is critical becuase it allows you to get an idea of the lower bounds of complexity for an algorithm. We typically bucket hardness into 4 different classes, P (Polynomial), NP (Non-deterministic Polynomail), NP-Hard, and NP-Complete. There are other complexity classes, but they are out of scope for these notes.

Before we dive into hardness we need to define some terms.

  • Reductions
    • A reduction, or reducing a problem means to modify one input into a form that can be solved

P

When we say a problem is in P, that means it can be solved in polynomial time, with respect to the input size. Concretely, given an input of size $N$, a problem can be solved in $O(N^{x})$, where $x$ is some constant value. The key thing here is that as long as the complexity is polynomial then it is in the class P.

NP

When a problem is in NP, that means we can verify a solution to the problem in polynomial time. That is, given some solution to a problem we can verify that the solution is correct in $O(N^{x})$, where $x$ is some constant value.

NP-Hard

A problem is considered NP-Hard if it can be solved on a Non-Deterministic machine in polynomail time. What that means in practice is that it can be solved in $O(x^N)$ time for some input of size $N$.

A key thing here is that all NP-Hard problems reduce to each other. This is useful becuase we can prove that a problem is in NP-Hard by reducing a known NP-Hard problem to the problem in question.

In order to prove that a problem is in NP-Hard we need to reduce a known NP-Hard problem to the target of the proof. Concretely, given a problem A, to prove it is in NP-Hard we must reduce a known NP-Hard probem B, to the problem A.

There are a few key components to the reductions done in this proof:

  • The transformation of the input for B must be done in polynomial time
  • The transformation of the output of A must be done in polynomial time
  • There is a solution for A if and only iff there is a solution for B

NP-Complete

A problem is considered NP-Complete if it is in both NP and NP-Hard. To prove a problem is in NP-Complete we need to prove that a problem is in both NP and NP-Hard.

Known NP-Complete problems

This is not an exhaustive exploration of NP-Complete problems, but the ones described here a very common and cover some of the most common reductions.

SAT

SAT, or satisfiability is the siminal NP-Complete probelm. Given a series of clauses in conjunctive normal form (CNF), with any number of variables or literals, return a satisfying assignemnt for each variable.

3-SAT

3-SAT is very similar to SAT, with one important constraint, each clause has at most 3 literals or variables.

Independent Set

Given an undirected Graph $G$, and an upper bound $B$, return a set of verticies where there is no edges between any of the verticies.

Clique

Given an undirected Graph $G$, and a lower bound $B$, return a set of vertices where there is an edge between every pair of verticies.

Vertex Cover

Given an undirected Graph $G$, and an upper bound $B$, return a set of verticies that cover all edges in the graph.

Subset Sum

Given a set of numbers $S$, and a budget $B$, return a set of numbers $R$ where $R$ is a subset of $S$ and the sum of all numbers in $R$ equals $B$.

Knapsack

Given a set of numbers $S$, a capacity $C$, and a budget $B$, return a set of numbers that sum